SAMG (Algebraische Mehrgitterverfahren für Systeme) ist eine Bibliothek von Unterroutinen zur hocheffizienten Lösung großer linearer Gleichungssysteme mit dünnbesetzten Matrizen. Solche Gleichungssysteme bilden den numerischen Kern der meisten Simulationssoftwarepakete.
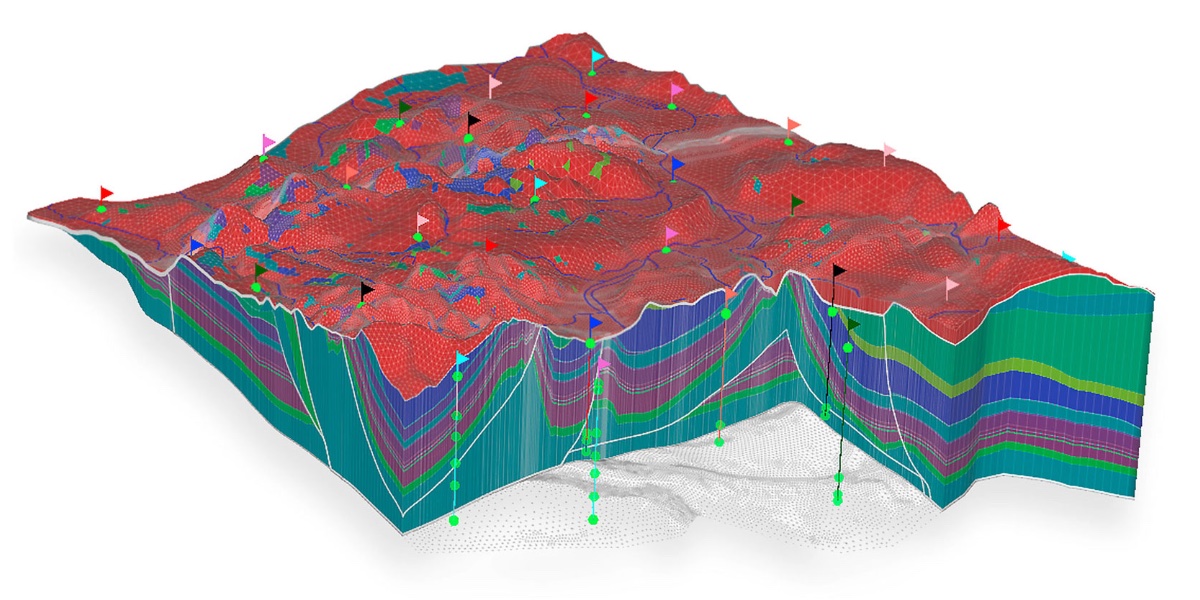
SAMG Grundwassersimulation | © DHI Wasy
Nutzen & Mehrwert
Gegenüber klassischen Verfahren (zum Beispiel durch ILU vorkonditionierten Verfahren der konjugierten Gradienten) hat SAMG den großen Vorteil einer weitestgehend numerischen Skalierbarkeit. Das bedeutet, dass der Rechenaufwand mit SAMG nur linear von der Anzahl der Unbekannten abhängig ist. Je nach Anwendung und Problemgröße kann der dadurch bedingte Rechenzeitgewinn ein bis zwei Größenordnungen ausmachen. Dabei lässt sich SAMG genauso einfach in ein existierendes Simulationspaket integrieren wie ein klassisches Verfahren.
Zielgruppen
Die SAMG Bibliothek ist interessant für alle, die Softwaretools zur Durchführung großskaliger numerischer Simulationen entwickeln oder anwenden. Zusätzlich zu unserer Lösertechnologie bieten wir auch Analyse und Beratung zu Anwendungsproblemen sowie die Anpassung unserer Software auf kundenseitig betriebene Rechnersysteme, speziell Parallelrechner, an.
Herausragende Eigenschaften von SAMG
In vielen Anwendungen der numerischen Simulation, zum Beispiel der Strömungs- und Strukturmechanik, werden die Strukturen und Geometrien durch komplexe Gitter diskretisiert. Je feiner ein solches Gitter ist, desto genauer ist im Allgemeinen die Simulation, umso größer sind aber auch die aus dem Diskretisierungsprozess resultierenden, numerisch zu lösenden Gleichungssysteme. Bei den heute erforderlichen Simulationsgenauigkeiten ist die Zeit, in der diese Gleichungssysteme gelöst werden können, eine kritische Größe. Klassische numerische Lösungsverfahren sind nicht in der Lage, die entstehenden großen Gleichungssysteme in einer ökonomisch vertretbaren Rechenzeit zu lösen.
Die Lösungsmodule von SAMG basieren auf modernen hierarchischen Verfahrensansätzen (algebraische Mehrgittermethodik, AMG): Anstatt nur mit dem gegebenen (extrem großen) Gleichungssystem zu arbeiten, kombinieren algebraische Mehrgitterverfahren die numerische Information in einer Hierarchie immer gröberer Gleichungssysteme, um das gegebene Problem schneller zu lösen. Der zugrunde liegende Vergröberungsprozess ist automatisch und für den Benutzer von SAMG transparent.
Kundenmeinungen
SAMG has been the key to improving both the robustness and performance of our General Purpose Research Simulator – GPRS. With SAMG as the workhorse linear solver, we now routinely solve problems that were simply beyond our reach. SAMG is indispensable for reservoir flow simulation of large-scale, highly heterogeneous, unstructured reservoir models.
For our applications, SAMG is the fastest solver in the world. SAMG has enabled us to tackle large problems faster than ever before and attempt larger problems that were ever possible – for the first time we can make multi-million cell simulations routine where we properly capture the reservoir structure.
SAMG is in a world of its own when it comes to linear solvers. It is robust, fast, and easy to implement on any platform, and has given our company a clear competitive edge. It has been a reliable work requiring little or no maintenance, allowing us to concentrate on our core business. Small or big, simple or complex, sparse or full, structured or unstructured – SAMG will solve it.